Besides the main program file, the code contains the following building blocks for topology optimization:
- TopOpt class containing mesh and optimization parameters.
- Physics class containing a 3D linear elasticity solver and objective, constraint and sensitivity computations.
- Filter class containing both standard and PDE based filters.
- MMA class with a simple, fully parallel implementation the method of moving asymptotes.
- IO class and Python script converters.
Examples obtained using the framework:
|
 
|
|
Optimization history for a 3D cantilever beam modelled with 130 million elements and 395 million state degree of freedom. Note that the visualization merely thresholds the design, i.e. no smoothening has been performed! The design was computed in 4 hours and 20 minuttes using 2000 cores (100 nodes each with 2 Intel-Xeon E5-2650 ten-core CPUs) and a total of 2000 design cycles.
|
|
|
|
|
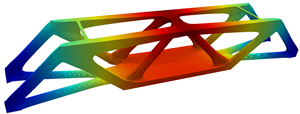
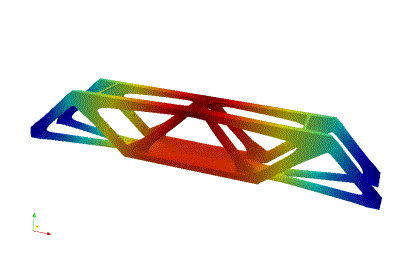
MBB Beam in 3D with 113 million elements and 348 million state degree of freedom.
|
Rotation of the MBB beam design.
|
|
|
 
|
|
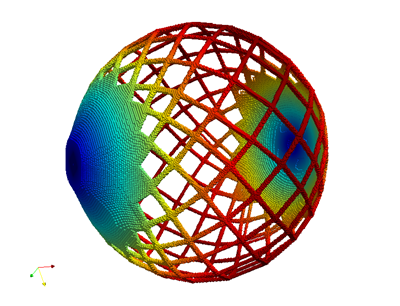
Design of a Michell sphere, i.e. a box loaded in pure torsion.
|
Rotating view of the Michell sphere.
|
|
|
 
|
|
Unit cell of an optimized 3D isotropic micro-
structure with a Poisson's ratio of -0.80.
|
3x3x3 unit cells of an optimized 3D isotropic micro-
structure with a Poisson's ratio of -0.80.
|
Descriptions of the parallelized MMA implementation and the PDE filters are discussed in the following papers:
[2] Aage N, Lazarov B (2013) Parallel framework for topology optimization using the method of moving asymptotes. Structural and Multidisciplinary Optimization 47(4):493–505, DOI 10.1007/s00158-012-0869-2
[3] Lazarov BS, Sigmund O (2011) Filters in topology optimization based on helmholtz-type differential equations. International Journal For Numerical Methods In Engineering
References to external codes/software:
[4] Balay S, Brown J, , Buschelman K, Eijkhout V, GroppWD, Kaushik D, Knepley MG, McInnes LC, Smith BF, Zhang H (2013) PETSc users manual. Tech. Rep. ANL-95/11 - Revision 3.4, Argonne National Laboratory
[5] Schroeder W, Martin K, Lorensen B (2003) The Visualization Toolkit, Third Edition. Kitware Inc.